Hallo Freunde,
eigentlich beschäftigte mich die nachstehende Frage schon bei der Dachausführung Höchstadt/Aisch. Nachdem es sich aber um eine generelle Frage für Häuslebauer handelt, würde ich sie gerne hier abklären und, bei entsprechender Lösung, hier abschließend darstellen.
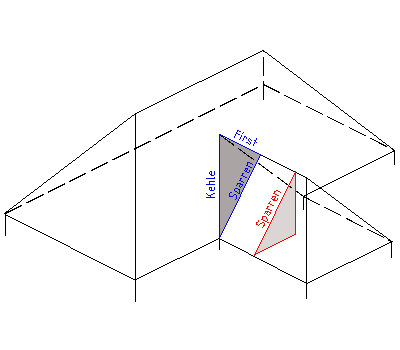
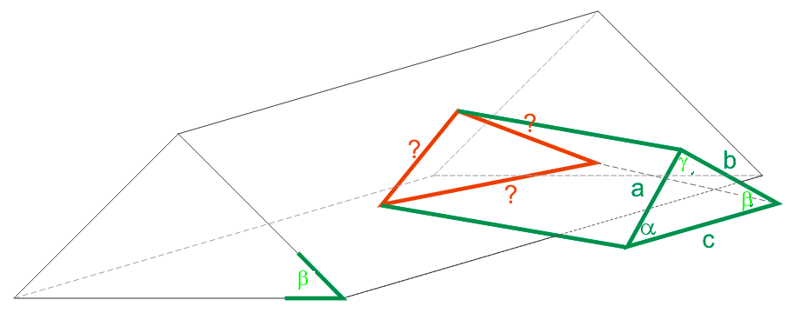
Viele Satteldächer haben Gauben, manche Zwerchhäuser. Immer dann, wenn die "Anbauten" ebenfalls Satlteldächer haben, fehlt mir eine Methode/Formel zur Berechnung des notwendigen Dachausschnittes im Hauptdach. Ich habe die Maße bisher mit Karton und "Annäherung durch abschneiden" ermittelt - das ist auf Dauer unbefriedigend. Zum besseren Verständnis meiner Frage, hier eine Zeichnung dazu. Wie ermittle ich die Maße a, b, c und alpha, beta, gamma des rot gezeichneten Dreieckes? ![]()
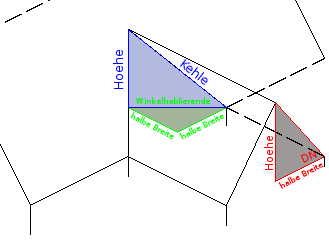
Die grün gezeichneten Elemente sind mit ihren Maßen bekannt.
Danke für Eure Unterstützung.
Gruß Rainer